Overview
As we bid farewell to Fibonacci Day this year, celebrated on 23rd November every year, let’s rewind the clock to history and delve into the mesmerising examples of the Fibonacci sequence unfolding daily in Mother Nature.
Brace yourself to be mind-blown as we unravel the enchanting illustrations of the Fibonacci sequence embedded in the very fabric of our natural world. Brace yourself for a post-Fibonacci celebration as we explore the fascinating tales written by nature in sunflowers’ spirals, pinecone arrangements, and much more. It might be the day after, but the magic of Fibonacci is timeless—the math is real, and believe us, it’s nothing short of astounding. Get ready to have your mind thoroughly blown.
What is the Fibonacci Sequence?
The concept of the Fibonacci sequence originates from the 13th-century Italian mathematician Leonardo Fibonacci. Beginning with 0 and 1, this numerical series unfolds in a constant progression, with each subsequent number being the sum of the two preceding ones.
For example, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377…
What is the Golden Ratio?
While not identical to Phi, the Golden Ratio shares a close connection. Entirely derived from the Fibonacci Sequence, it emerges from a relationship between two consecutive numbers in the Fibonacci sequence. Divide the larger number by the smaller one, and you’ll get a result approaching Phi. As you progress through the Fibonacci Sequence, the outcomes draw nearer to Phi, although they never precisely match. This is because irrational Phi cannot be expressed as a fraction.
The History of the Fibonacci Series
The origins of the Golden Ratio trace back to a sequence of numbers that has intrigued mathematicians since around 300 BCE. The journey began with Acharya Pingala, an ancient Indian poet and mathematician, who observed a pattern of short and long syllables in lines of Sanskrit poetry.
This pattern was later translated into a sequence of numbers known as the mātrāmeru.
Fast forward about 1500 years, and the same series earned the name Fibonacci sequence. Today, the all-encompassing influence of this sequence is evident in emergent patterns and ratios, such as Phi (1.61803…). These patterns resonate across scales, from the microscopic to the cosmic, manifest in biological systems and inanimate objects.
The Floral Realm
In the world of flowers, a fascinating numerical rhythm unfolds, and it’s all tied to the Fibonacci sequence. Picture it as a natural dance where flowers follow a specific petal count, guided by this ancient mathematical pattern. Lilies opt for three petals, buttercups boast five, chicory steps up with 21, and daisies steal the spotlight with an impressive 34 petals.
What’s the secret behind this floral arrangement phenomenon?

It’s all about Phi, the divine proportion. Each petal strategically takes place at 0.618034 per turn within 360 degrees or a full circle, a design choice honed by the forces of evolution. This precision ensures the best exposure to sunlight and other crucial factors.
But the Fibonacci magic doesn’t stop at petals—it extends to the very heart of the flower, the seed head. Picture seeds taking centre stage and gracefully moving outward to fill every available space. Sunflowers showcase this beautifully with their mesmerising, spiralling patterns. It’s nature’s way of choreographing a mathematical masterpiece, visible in petals and seed heads.

Likewise, the enchanting world of nature continues its mathematical symphony in the arrangement of seed pods on a pinecone. Consider a 3-5 cone where the spirals meet at the back after three steps along the left spiral and five steps along the right. It’s nature’s way of incorporating the Fibonacci sequence into the very structure of pinecones.
Space
Would you believe it? Like our Milky Way, even galaxies follow a pattern akin to the Fibonacci sequence. Picture the Milky Way with its swirling arms, each forming a graceful spiral of about 12 degrees.

But here’s where it gets interesting: despite what we’d expect from classic physics, galaxies have a bit of a quirk. Astronomers noticed this in 1925 and dubbed it the “winding problem.” According to the rules, as galaxies spin, their arms should start to wind around the centre. But guess what? They don’t.
It’s like a cosmic magic trick—the stars on the outer edges of these spirals move faster than we’d predict. This unique cosmic twist keeps the galaxy’s shape intact, challenging our understanding of how things should work in space. It’s a bit of a celestial mystery, with scientists and space enthusiasts gazing up at the night sky, wondering about the secrets these galaxies hold.
Hurricanes
Amid a hurricane’s fury lies a peculiar calm—the eye of the storm. It’s more than just a temporary respite; it’s a crucial moment, a breaking point where the winds temporarily cease before resuming their relentless course. Now, picture this eye as the origin of a mathematical sequence, much like the 0 or 1 in the Fibonacci sequence.
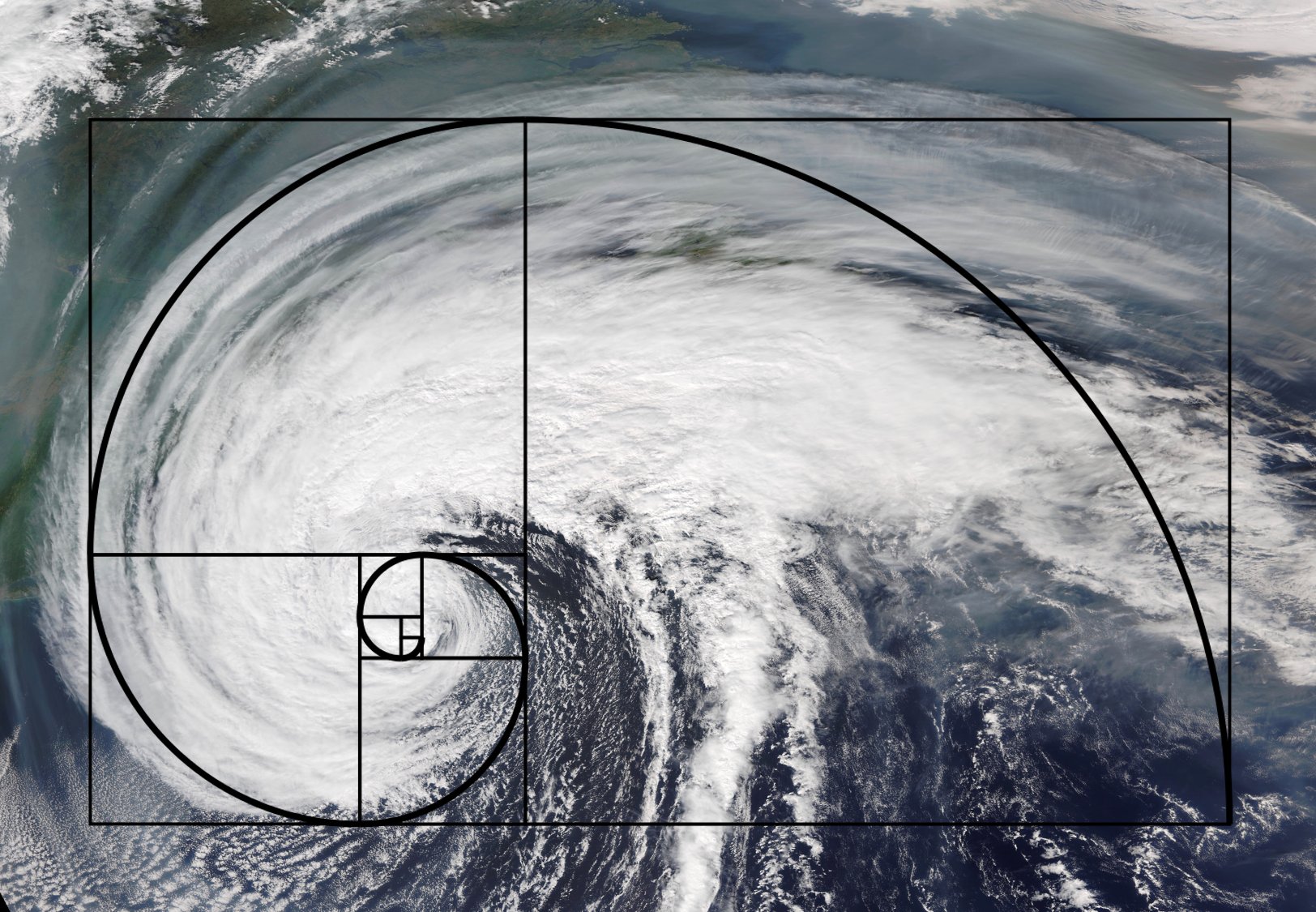
As you navigate the hurricane’s counterclockwise spiral, there’s a fascinating consistency—a steady increase akin to the rhythmic progression in the Fibonacci sequence. This natural phenomenon unfolds in a pattern reminiscent of the elegant Golden Ratio, weaving a captivating narrative of chaos and order.
Humans
Faces, whether human or otherwise, carry the subtle signature of the Golden Ratio. Take a glance, and you’ll find the mouth and nose carefully positioned at golden sections between the eyes and the chin. These harmonious proportions extend even when viewed from the side, and the look and ear follow a captivating spiral that traces the Golden Ratio.
It’s essential to acknowledge that everyone’s body is unique, but these proportions tend to lean towards Phi on average.
Interestingly, there’s a notion that the closer our features align with the Golden Ratio, the more “attractive” they are perceived to be. For instance, the most aesthetically pleasing smiles often showcase central incisors that are 1.618 times wider than the lateral incisors, continuing in a harmonious sequence.
From an evolutionary psychology perspective, this preference might be hardwired into us as an indicator of fitness and health.
Shifting our gaze to our hands, the lengths of our fingers follow a similar dance. Each section, from tip to wrist, expands roughly aligned with the ratio of Phi. Not only that! Surprisingly, the proportion of our hand to our forearm ends up at 1.618, too! The examples go on: the leg to the length from the knee, and The human ear forms a Golden spiral.
DNA

The microscopic world, it seems, is not exempt from the enchanting grip of Fibonacci. Take the DNA molecule, for instance. Its double helix spiral, the essence of life’s blueprint, unfolds in a pattern that echoes the Fibonacci series. Each complete cycle measures 34 angstroms in length and 21 angstroms in width.
The magic lies in the numbers themselves—34 and 21 are Fibonacci series members. Dive deeper into their relationship, and you’ll find their ratio, 1.6190476, is a close match to Phi, the divine proportion, at 1.6180339. It’s as if the intricate dance of life, even at the microscopic level, follows a mathematical rhythm that weaves the beauty of Fibonacci and the allure of the Golden Ratio into the very fabric of our existence.
Honey Bees
Honey bees, those industrious little creatures, seem to have a knack for incorporating Fibonacci into their lives in fascinating ways. Let’s start with the gender ratio in a colony—females always outnumber males. When you divide the number of females by the number of males, the result typically lands remarkably close to 1.618, the magical Phi.
Now, peek into the family tree of honey bees, and you’ll discover another Fibonacci-inspired tale. Males have a single parent (a female), while females have two—a female and a male. This sets the stage for a generational dance: males have 2, 3, 5, and 8 grandparents, great-grandparents, gr-gr-grandparents, and gr-gr-gr-grandparents, following the Fibonacci pattern. Following suit, females have 2, 3, 5, 8, 13, and the sequence continues.

And if that wasn’t enough, even bee physiology plays along with the Golden Curve quite gracefully. It’s as if nature has woven Fibonacci into every aspect of the honey bee, turning its tiny world into a marvel of mathematical harmony.
Conclusion
In conclusion, the Fibonacci sequence and the Golden Ratio aren’t just abstract mathematical concepts; they’re the hidden threads weaving through every corner of our existence. From the grandeur of galaxies to the delicate details of honey bee colonies, it becomes clear that math is not confined to textbooks; it’s everywhere and a silent but awe-inspiring architect of our natural world.











